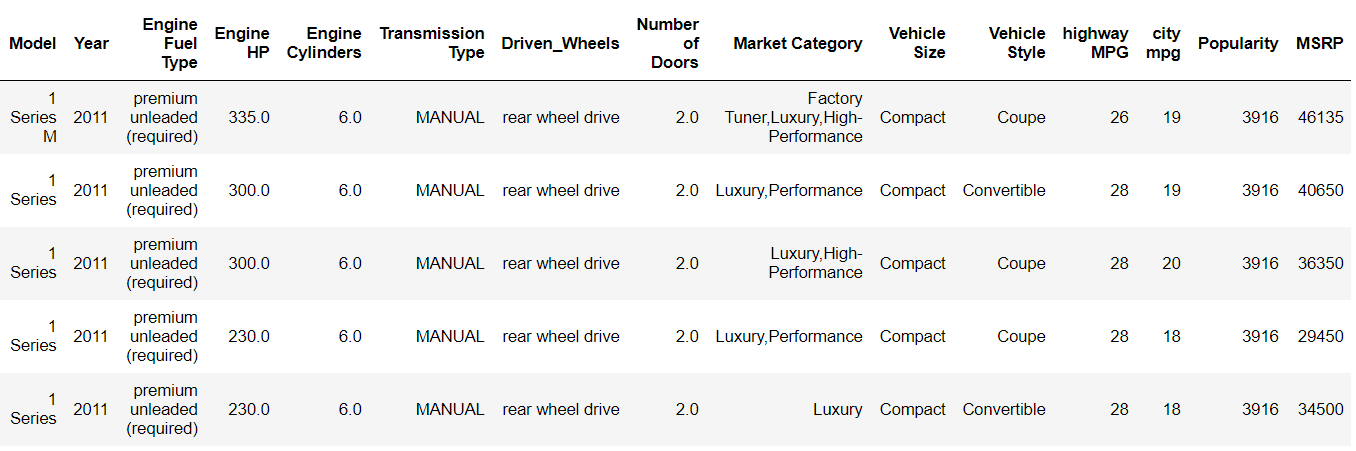
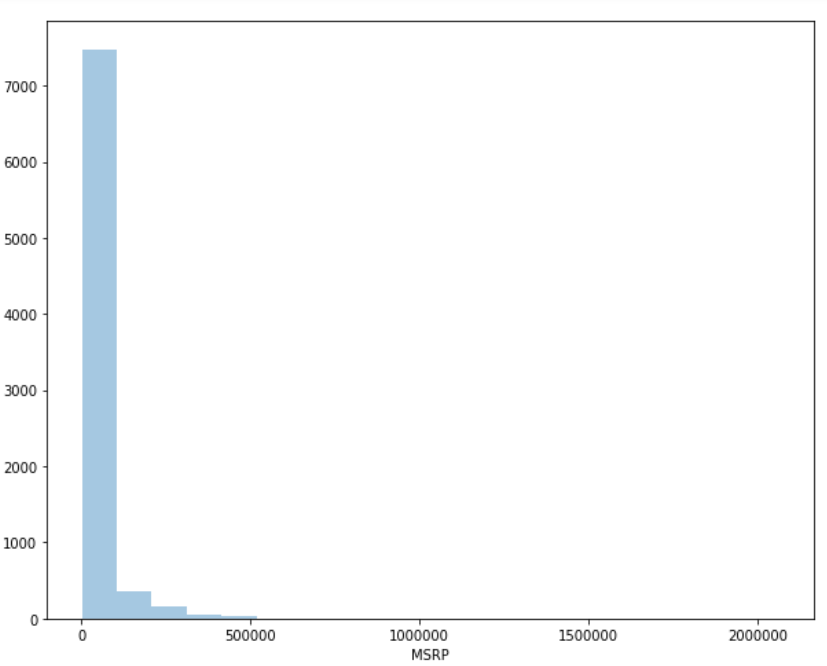
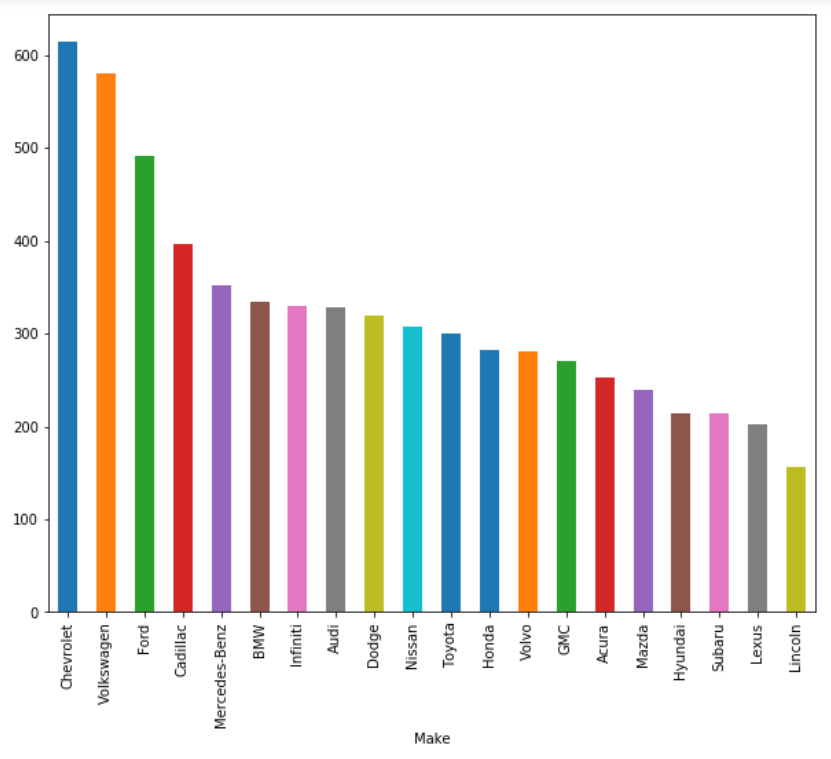
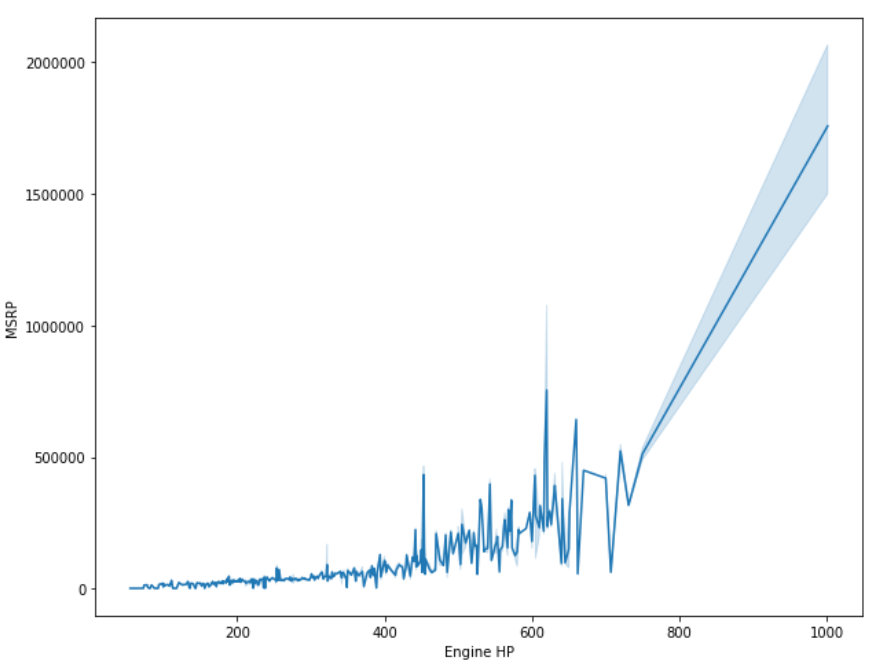
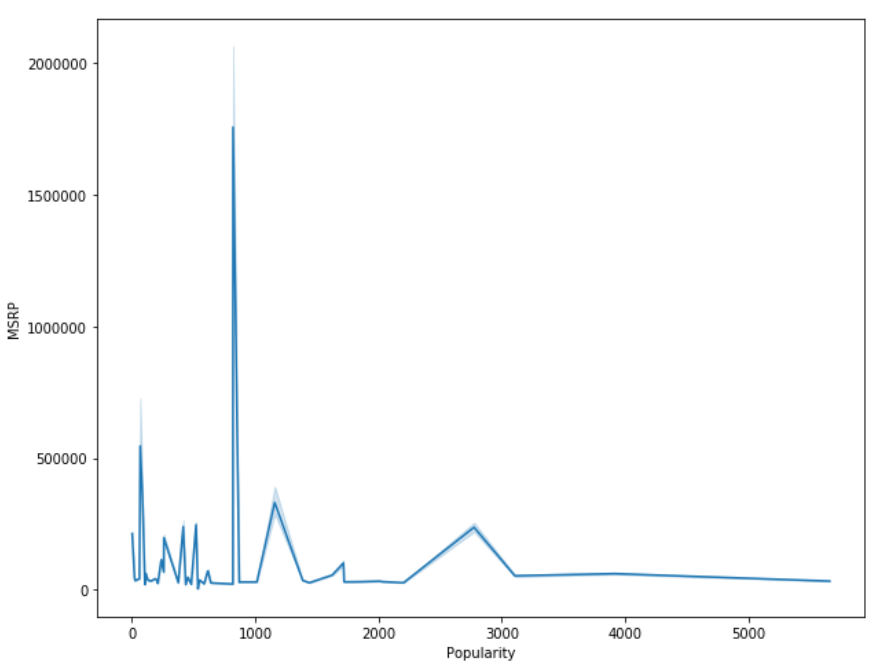
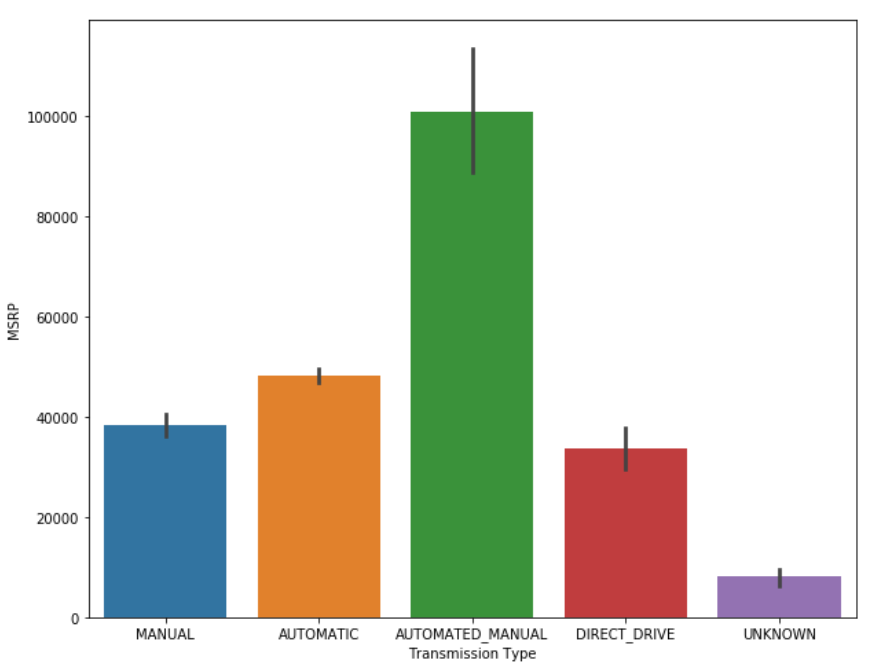
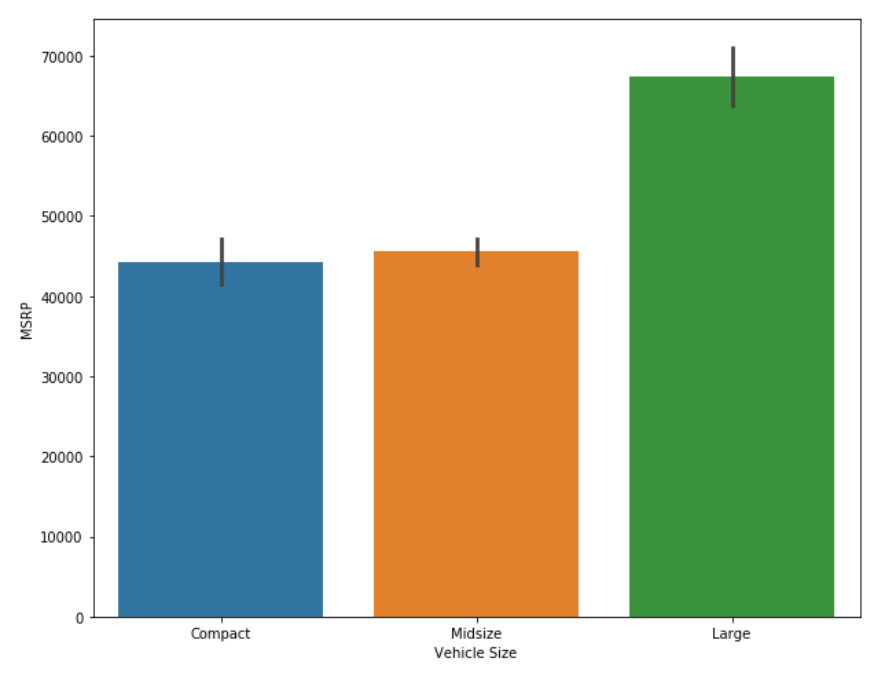
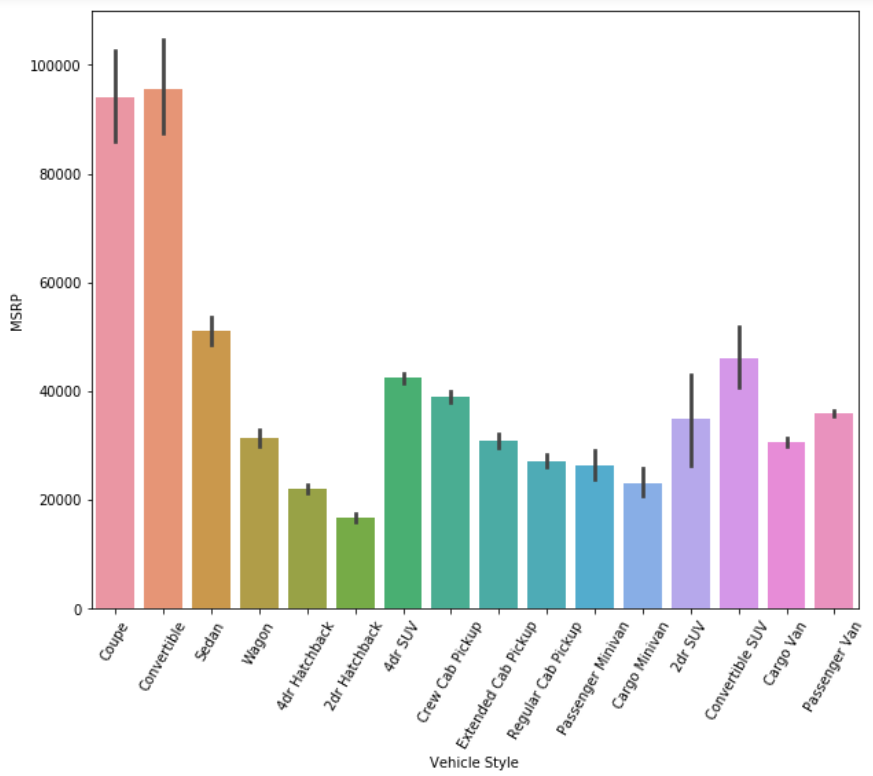
However, there are still cases where traditional machine learning algorithms are significantly ahead of artificial neural networks. Particularly in the case of smaller datasets, machine learning techniques are still handsomely outperforming the deep learning approaches.
In this article, we will develop statistical models capable of predicting the price of used cars. We will develop two models. One of the models will be trained used Random Forest Algorithm which is one of the most commonly used traditional machine learning model and the other model will be trained using a deep neural network. We will compare the performance of both the models and see which model is more suited for used car price prediction.
The dataset we used for developing the model is freely available at the following kaggle link.
https://www.kaggle.com/jshih7/car-price-prediction/data
Download the dataset and place it in one of your local directories.
Given different attributes of a used car such as the engine horsepower, year of manufacture, number, transmission type, vehicle size, and style we have to predict the price of the vehicle. To train and test the algorithms, the MSRP (Manufacturer Suggested Retail Price) for each car is also available. This is a supervised learning problem where the outputs are already given. We just have to train our models using the training data and evaluate the models on the test data.
To solve this problem, we will develop two models, one using the Random Forest algorithm and other using a deep neural network. We will then see which algorithm predicts car prices with higher accuracy.
We will follow the traditional machine learning steps to solve the problem.
Importing Libraries and Dataset
As always the first step is to import the required libraries and the dataset. The following script imports the necessary libraries.
And the following script imports the dataset:
In the above script, we first import the dataset and then remove all the records having null values from the dataset.
Let’s how our dataset looks. We can use the “head()” method of the dataframe to view the first five rows as shown below:
The next step is to analyze the dataset. Let’s first see the price distribution for all the cars. We will use the Seaborn library for plotting our plots. Before we plot actual graphs, let us change the default graph size to have a better view. The following script increases the default graph size:
As a first step of the data analysis, let’s first look at the price distribution for each class. Execute the following script:
From the output, you can see that price of most of the cars range between 0 – 100,000.
Let’s now see who the top 20 car manufacturers in our dataset are. Execute the following script:
The output shows that most of the cars in the dataset are manufactured by Chevrolet, followed by Volkswagen and Ford.
Normally the cars with higher engine horsepower are costlier than those with lower engine horsepower. Let’s plot the relationship between engine horsepower and the price of the car to see if we can find any positive correlation. Run the following script:
We can clearly see a somewhat positive correlation and the price of the car.
Let’s now plot the relationship between the popularity of the car and the price of the car.
From the output, it is evident that cars that have high popularity among the public is not necessarily expensive. Cars that are fuel efficient, economic and comfortable are generally more popular among the public as compared to the high-end luxury cars.
Next, let’s plot a bar plot for the transmission type and car prices.
The results show that on average, cars with automatic transmission are slightly expensive than cars with manual transmission. The cars with both automatic and manual transmission are clearly most expensive of all the car types.
Similarly, let’s plot the relationship between vehicle size and the car price.
The result reflects the fact that large vehicles are normally priced higher as compared to midsize and compact vehicles.
As a final data analysis step, let’s plot the relationship between car style and the car price.
The output shows that coupe, convertible and sedan style vehicles are on average more expensive than the rest of the vehicles.
As the first step in the preprocessing phase, we will remove the Make and Model columns from our dataset since they contain too many unique values and hence are not very useful indicators of vehicle price. The following script removes the Make and Model columns.
In our dataset, the ‘Engine Fuel Type’, ‘Transmission Type’, ‘Driven_Wheels’, ‘Market Category’, ‘Vehicle Size’, and ‘Vehicle Style’ columns are categorical columns that contain data in the form of text. However, machine learning algorithms work with statistical data. We convert categorical data into numerical data using one-hot encoding scheme. The idea is to remove the categorical column and add one column for each of the unique values in the removed column. Then add 1 to the column where the actual value existed and add 0 to the rest of the columns.
The following script removes categorical columns from the dataset:
The following script converts categorical columns into one hot encoded vectors:
Finally, the following script concatenate the actual data set without actual categorical columns with the one hot encoded version of the categorical columns:
As the next preprocessing step, we divide our data into label and feature set:
And finally, before we train and evaluate our models, we need to divide the data into training and test sets. Look at the following script:
As we said earlier, we will use a deep neural network and random forest algorithm to compare the performance of our algorithms.
Let’s first train the Random Forest model to see how well the trained model performs. Execute the following script:
We trained our model on the training set using the “fit()” method of the RandomForestRegressor class from the sklearn.ensemble module.
Next, we need to make predictions on the test set. To do so, execute the following script:
Now our model has been trained, the next step is to evaluate the performance of the model. The metrics used for the evaluation of regression models are root-mean-square error (RMSE), mean squared error (MSE), and mean absolute error (MAE). The following script finds the value for these metrics for the linear regression algorithm:
The results for the Random Forest Algorithm are as follows:
The second test is performed using the deep neural network with three layers of 100 nodes. The following script trains the deep neural network on training set and makes prediction on the test set.
And the following script evaluates the performance of the deep neural network:
The results for the deep neural network are as follows:
From the performance results obtained using Random Forest and the Deep Neural Network, we can safely assume that the Random Forest algorithm outperforms the Deep Neural Network for predicting car prices. The values for all the performance metrics e.g. MAE, MSE and RMSE are smaller for the Random Forest algorithm than the Deep Neural Network which reflects the suitability of the Random Forest Algorithm for used car price prediction.
One of the reasons that the Random Forest Algorithm outperformed Deep Neural Network is the size of the dataset. We only had 11 thousand records in the dataset. After removing null values we are left with around 8800, records which is not a sufficient number to train a deep neural network. Therefore, the Random Forest Algorithm outperformed deep neural network in this case.
